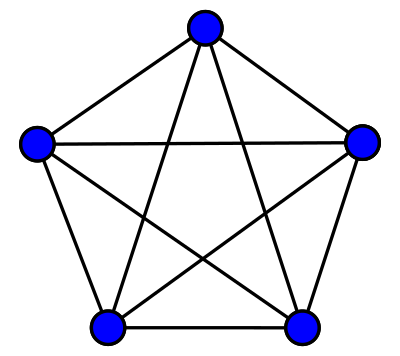
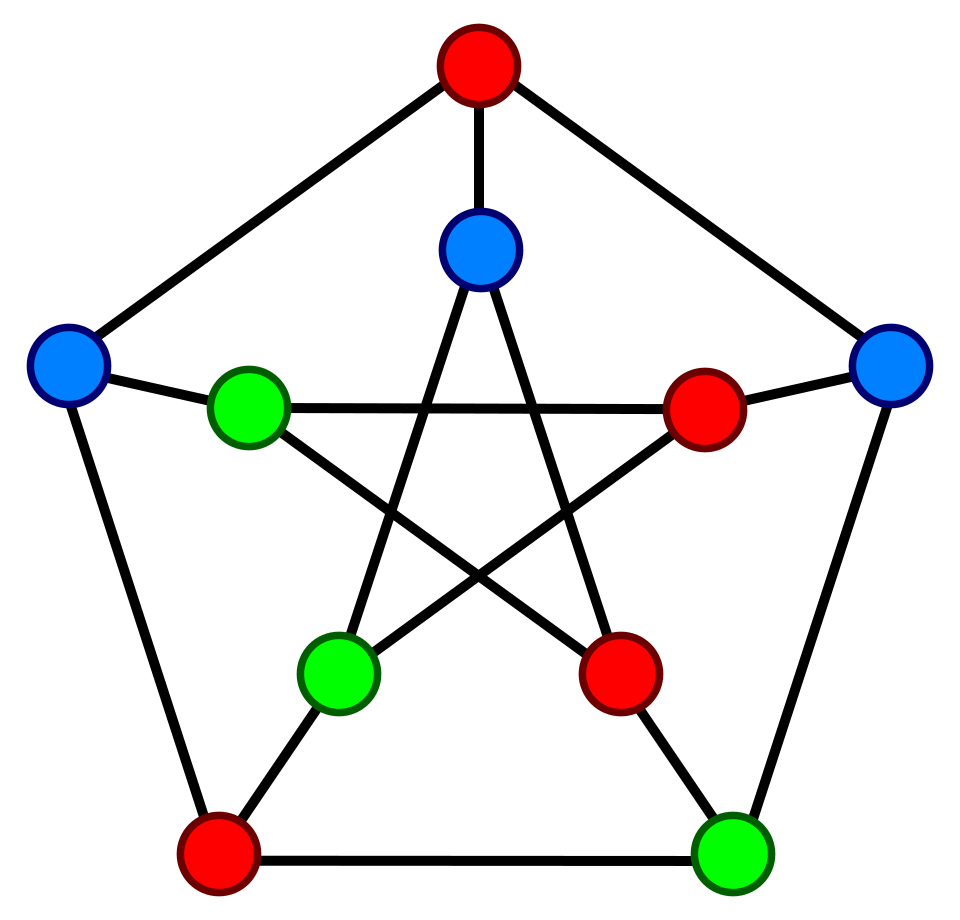
isomorfismo en grafos
En teoría de grafos, un isomorfismo de grafos es una biyección de los vértices de un grafo sobre otro, de modo que se preserva la adyacencia de los vértices. Más formalmente, el isomorfismo entre dos grafos G y H es una biyección f entre los conjuntos de sus vértices que preserva la relación de adyacencia.1 Es decir, cualquier par de vértices ...